Détection d'erreurs et signatures électroniques

Un premier MON s'intéressant à l'intégrité des données (d'un point de vue informatique) : sommes de contrôles, hash, signatures numériques...

☰

Dans ce MON, premier de deux dédiés à des questions d'intégrité des données, j'explore deux moyens de vérifier si des données peuvent être considérées commes fiables : la détection d'erreurs, qui permet de savoir si les données ont été transmises correctement, et les signatures électroniques, qui permettent de s'assurer de l'origine des données. Je m'intéresse principalement ici aux aspects informatiques, mais il est important de noter qu'il existe bien d'autres aspects à l'intégrité des données : ces méthodes sont inutiles sans un contrôle de la fiabilité de la source, si les données envoyées sont incorrectes (dans un sens plus large) dans un premier lieu, ou bien évidemment si elles ne sont pas mises en place.

L'intégrité des données, kézaco ?

La notion d'intégrité des données dans le monde de l'entreprise se réfère en général aux principes ALCOA++ (de l'anglais Attribuable, Legible, Contemporaneous, Original, Accurate, auxquels s'ajoutent Complete, Consistent, Enduring, Available et Traceable). Cependant, comme précisé en introduction, je vais m'intéresser ici au sens informatique de l'intégrité des données. Si on veut faire le lien avec ALCOA, ça correspond en gros aux principes d'Originalité, s'assurer que les copies des données sont des copies conformes, et d'Attribution, savoir de qui viennent les données.

Plus précisément, ici le but va être de s'assurer que, lors d'une transmission de données, on puisse savoir :

• s'il y a eu des erreurs lors de la transmission, et donc des informations perdues ou modifiées.
• que les données proviennent bien de la personne (ou du système) de laquelle elles sont censées venir.

Détecter les erreurs

On peut s'attaquer au problème de la détection d'erreurs sous deux angles : le domaine des communications va principalement s'intéresser aux erreurs de transmission, à priori aléatoires, tandis que la cryptographie va considérer un adversaire intelligent qui cherche à modifier les données transmises pour son intérêt personnel sans être détecté. En pratique, les méthodes de la cryptographie détectent aussi bien les erreurs aléatoires de transmissions, mais demandent beaucoup de calcul, donc des méthodes plus simples restent intéressantes quand des propriétés cryptographiques fortes ne sont pas nécessaires.

Les idées de base

Le principe général de la détection d'erreurs va être de donner une information supplémentaire sur les données, en général le résultat d'un calcul sur ces données. Ainsi, à la réception, le destinataire peut effectuer le calcul et vérifier s'il obtient le même résultat. On parle alors de redondance, puisque ces informations peuvent se déduire des données. Selon le contexte, cela peut se faire de deux façons :

• soit en ajoutant une "clef" aux données afin que le résultat attendu soit indépendant des données. Ce sont par exemple les deux derniers chiffres du numéro de sécurité sociale en France, ou le dernier chiffre des ISBN, les numéros d'identification des livres.
• soit en présentant ce résultat "à côté" des données. En général, c'est employé par exemple pour les téléchargements de fichiers, tels que des images disques de ditributions Linux. (Par exemple Debian ci-dessous, les fichiers SHA256SUMS ET SHA512SUMS contiennent ce résultat pour les 3 autres fichiers. Il y a également deux fichiers floutés, qui nous serviront plus tard...)

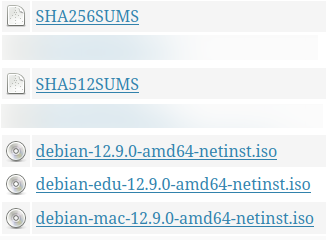
Évidemment, les deux possibilités ont leurs avantages et inconvénients. Ainsi, la première permet une transparence totale pour l'utilisateur, puisque la détection des erreurs est très facile à automatiser, mais en contrepartie ne présente aucun intérêt cryptographique : un attaquant n'a qu'à modifier la clef ajoutée pour maintenir le résultat correct. De plus, il faut que ce soit prévu par les systèmes qui interagissent avec ces données, pour qu'ils ne gardent que les données "réelles". La deuxième méthode corrige donc, au moins en théorie, ces inconvénients : les données et le résultat sont transmis séparément, donc il est moins facile de les modifier d'une manière cohérente (enfin, la question se pose si les deux sont stockés au même endroit), et il n'y a pas le risque qu'une clef soit considéré comme des données. C'est d'ailleurs pour cela qu'on l'utilise quand il faut vérifier un téléchargement de fichier : on ne peut pas ajouter des données à un fichier arbitraire, puisqu'on ne sait pas comment elles seront interprétées par les logiciels qui liront ce fichier. Cependant, cela nécessite que l'utilisateur fasse la vérification manuellement.

Des algorithmes et exemples simples

Je vous ai parlé des numéros de sécurité sociale et des ISBN, qui utilisent des calculs simples, et feront donc des bons premiers exemples, avant de s'intéresser aux algorithmes plus complexes qui s'appuient notamment sur la représentation binaire des données et des opérations mathématiques sur des objets plus exotiques que nos nombres habituels écrits en base 10. Je ne traiterai en détail que ces cas simples, pour éviter de trop alourdir ce MON avec des mathématiques incompréhensibles, mais ils permettront d'illustrer les grands principes sur lesquels se baseront les algorithmes plus avancés.

Le numéro de sécurité sociale

Commençons par le numéro de sécurité sociale, c'est probablement celui dont le calcul est le plus simple : vous prenez les 13 premiers chiffres, et vous calculez le reste dans la division euclidienne par 97. Les deux derniers chiffres seront tout simplement la différence entre 97 et ce reste. Ainsi, prenons le numéro de sécurité sociale commençant par les 13 premiers chiffres suivants (pris "au hasard", il n'existe normalement pas réellement) : 2 12 05 13 362 219. Cela nous donne le nombre à 13 chiffres 2 120 513 362 219. En faisant la division euclidienne, on trouve 2 120 513 362 219 = 21 860 962 497 * 97 + 10. On retranche donc à 97 le reste de 10, et on obtient comme clef 87, donc le numéro complet sera 2 12 05 13 362 219 87.

On retrouve déjà deux opérations qui seront très communes : prendre le reste dans la division euclidienne par un nombre n, et prendre la différence entre n et ce reste. Dans la suite, ce reste sera appelé "le reste modulo n", et cette différence sera "le complément modulo n". Une seule différence : avec ce formalisme, si la différence vaut n, le complément sera 0 au lieu de n.

ISBN-10 et ISBN-13 (ou EAN 13)

Jusqu'en 2007, on utilisait des numéros ISBN-10, à 10 chiffres, mais dans un souci de standardisation, on est passé en 2007 aux numéros ISBN-13, à 13 chiffres, qui sont en fait des numéros GTIN-13, un standard international qui s'applique en pratique à tous les produits, pas uniquement les livres. Ces deux systèmes utilisent un calcul différent pour leur clef, donc autant traiter les deux !

Tout d'abord, l'ISBN-10 : on prend les 9 premiers chiffres, et on multiplie le premier par 10, le second par 9, etc. On fait la somme, puis on prend son complément modulo 11. Le dernier chiffre devient alors ce complément (si le complément vaut 10 la clef est notée X). Ce calcul présente un avantage par rapport à celui du numéro de sécu : si on refait la même somme que pour trouver la clef, mais en continuant avec le dixième chiffre, càd la clef, que l'on multiplie donc par 1, on obtient un multiple de 11 ! Prenons là encore un exemple : l'édition originale de 1984 par George Orwell. Son ISBN est 0-45-228423-6. Le calcul de la somme pour les 9 premiers chiffres donne 10*0 + 9*4 + 8*5 + 7*2 + 6*2 + 5*8 + 4*4 + 3*2 + 2*3 = 170 = 15 * 11 + 5. Le reste est de 5, la clef (le dernier chiffre) est bien 11 - 5 = 6 !

Quant aux ISBN-13, ou EAN-13, le calcul devient plus complexe à expliquer, mais le principe reste similaire : vous prenez les 12 premiers chiffres, multipliez les chiffres aux positions impaires (en commençant par le chiffre le plus à gauche comme numéro 1) par 1, et les chiffres aux positions paires par 3. La clef est alors le complément modulo 10. On remarque que, là encore, si on applique le même calcul en incluant la clef, qui est alors le 13ième chiffre, on obtient un reste modulo 10 qui vaut 0. Prenons ici comme exemple le dernier livre de Judith Butler, Who's Afraid of Gender?, dont l'ISBN-13 est 978-0374608224. Les chiffres aux positions impaires sont 9, 8, 3, 4, 0 et 2, les chiffres aux positions paires sont 7, 0, 7, 6, 8 et 2. La somme nous donne 1 * (9 + 8 + 3 + 4 + 0 + 2) + 3 * (7 + 0 + 7 + 6 + 8 + 2) = 116 = 11 * 10 + 6, et la clef est bien 10 - 6 = 4.

Cette opération de prendre le reste dans une division euclidienne est très importante : l'idée est de condenser un potentiellement très grand nombre en un nombre de taille connue et relativement faible. En cryptographie, les fonctions qui réalisent une telle opération sont appelées des fonctions de compression, et c'est autour d'elles que repose la détection d'erreurs.

La parité

Nous allons maintenant nous intéresser aux données sous une représentation binaire. La raison est très simple : tous nos ordinateurs fonctionnent avec des représentations binaires, donc autant exploiter les propriétés de cette représentation dans nos calculs !

On va commencer par une idée très simple, et le dernier exemple que je traiterai en détail : la parité. Quand une donnée est écrite sous forme binaire, donc avec des "bits" valant uniquement 0 ou 1, la parité (informatique) de cette donnée est tout simplement la parité (mathématique) du nombre de 1 dans son écriture. S'il y a, mettons, 163 fois le chiffre 1, le nombre de 1 est alors impair, et on va dire que la parité de la donnée est de 1. S'il y a 38 fois le chiffre 1, le nombre de 1 est alors pair, et la parité de la donnée est de 0. Notre clef est alors tout bêtement la parité, 0 ou 1, que l'on ajoute encore une fois à la fin. Et là encore, on remarque que, en ajoutant la clef, le nombre de chiffres 1 sera toujours pair. Ainsi, disons que l'on souhaite envoyer le nombre 237. En binaire, il s'écrit 11101101. Il y a 6 1 et 2 0, la parité est donc paire, et on ajouterait un 0 à la fin.

Cette méthode n'est pas utilisée à de grandes échelles, parce qu'elle a une grande faiblesse au vu des quantités de données traitées : si un nombre pair de bits changent, le nombre de chiffres 1 ne change pas, donc elle n'est utilisable que quand la probabilité de changement d'un bit est faible par rapport au nombre de bits transmis. Cependant, elle reste parfois utilisée dans le cadre des communications au sein de systèmes électroniques, où les quantités de données échangées sont dans l'ordre de quelques dizaines de bits à la fois, par exemple avec le protocole RS-232. De plus, c'est la base de nombreuses méthodes qui consistent à calculer plusieurs parités pour détecter plus d'erreurs.

Les sommes de contrôle

Ces derniers exemples sont en fait ce que l'on appelle des sommes de contrôle (ou checksum en anglais) : on divise les données en petits bouts qu'on va sommer, puis on prend le reste dans une division euclidienne pour limiter la longueur du résultat. (On peut en effet interpréter la parité comme la somme des bits modulo 2.)

En fait, mathématiquemet, cela correspond à des additions dans un groupe fini : un ensemble fini de nombres sur lesquels on a défini une opération qui se comportent comme l'addition que l'on connaît bien sur les nombres réels. En prenant d'autres groupes finis, on peut définir de façon similaire des sommes de contrôles qui opèrent sur de nombreux bits à la fois : c'est par exemple le cas des sommes de Fletcher ou des sommes d'Adler (qui ont chacune différentes versions opérant sur des nombres de bits différents), ou de la somme de contrôle utilisée pour les paquets de données que se transmettent les ordinateurs sur Internet, avec le protocole TCP.

Cependant, faire simplement la somme sans une forme de pondération dépendant de la position pose un problème : puisque l'addition est commutative, on peut changer l'ordre de ces petits bouts ou en rajouter des "nuls" (qui valent 0) sans changer la somme de contrôle finale ; c'est pour cette raison qu'on retrouve ces multiplication pour les ISBN. (À noter qu'elles peuvent se réécrire comme des sommes, puisque l'on multiplie par un nombre entier, donc il est quand même correct de parler de somme de contrôle.)

Les contrôles de redondance cyclique (CRC)

Je vais passer rapidement sur cet ensemble de codes détecteurs d'erreurs, puisqu'ils reposent sur des concepts mathématiques assez abstraits et que Ben Eater a selon moi très bien vulgarisés dans cette vidéo.

Je tiens cependant à mentionner quelques-uns de leurs intérêts :

• Ils sont très efficaces pour détecter les erreurs sur de nombreux bits d'affilés, qui sont particulièrement communes en télécommunications, puisque la plupart des causes d'erreurs durent plus que la durée d'un bit : interférences, perte de connexion...
• Ils sont faciles à calculer au fur et à mesure de la réception des bits.

C'est une très grand famille, et ils ont eu (et ont toujours) de très nombreuses utilisations : dans les fichiers PNG, les protocoles Wi-Fi et Ethernet, des algorithmes de compression de fichiers, des systèmes de fichiers... Je ne peux pas faire une liste complète, mais un coup d'œil à la page Wikipédia devrait vous donner une assez bonne idée.

Les fonctions de hachage (cryptographiques)

Les fonctions de hachage, en règle générale, ont pour but de condenser des données en une "empreinte" courte, appelée "hash" ou encore "digestat", qui permet de les distinguer facilement d'autres données. En cela, toutes les méthodes précédentes utilisent des fonctions de hachage, mais qui présentent un inconvénient majeur : il est facile de modifier les données d'une façon qui n'impacte pas leur résultat, et qui est donc indétectable. C'est là qu'interviennent les fonctions de hachage dites cryptographiques.

Ces fonctions de hachage cryptographiques cherchent à corriger ce problème en utilisant des opérations qu'il est difficile d'inverser. D'autres étudiants de Do_It en ont déjà parlé, mais principalement dans le contexte du hachage de mots de passe (Thibault Adelain dans son MON 1.1) ou de la blockchain (Antoine Varnerot dans son MON 3.1, Victor Ory dans son MON 3.1 également), mais pas seulement, puisqu'Emma Gonin, dans son MON 1.2 a brièvement abordé le principe de hachage cryptographique pour les fichiers et autres messages, avec une magnifique infographie de la CNIL, que je vous invite à aller regarder.

Emma mentionne dans son MON les fonctions MD5 et SHA-1, qui sont, comme elle l'indique, considérées comme obsolètes du point de vue de la cryptographique, mais encore largement utilisables pour la simple vérification de l'absence d'erreurs de transmissions. De nos jours, pour des applications cryptographiques, on va plutôt utiliser des fonctions de la famille SHA-2 (SHA-256, SHA-512, SHA-224...), sauf par exemple pour les mots de passe et autre secrets d'authentification, qui sont généralement de petite taille, pour lesquels on privilégiera des fonction de hachage qui prennent longtemps à calculer.

Au-delà de leur utilité pour identifier les modifications de messages, ces fonctions de hachage cryptographiques ont une autre utilité : les signatures numériques.

Les signatures numériques

Là encore, Emma Gonin les a mentionnées rapidement dans son MON, mais sans expliquer le fonctionnement. Comme le montre l'infographie de la CNIL, les signatures numériques reposent sur la cryptographie asymétrique : chacun possède une clef dite "privée" et une clef dite "publique", liées entre elles et qui permettent respectivement de chiffrer et déchiffrer des messages (la clef publique déchiffrant les messages signés par la clef privée associée). Une signature numérique consiste alors à chiffrer le digestat du message à envoyer, et envoyer ce digestat chiffré avec le message. Le destinataire peut alors calculer le digestat du fichier, déchiffrer le digestat calculé par l'expéditeur, et vérifier s'ils correspondent.

Elles sont par exemple utilisées dans le système d'emails ou par git, pour signer respectivement des mails ou des commits git à l'aide de clefs OpenPGP, mais également par de nombreux distributeurs de logiciels afin de garantir l'authenticité des logiciels : Windows avec des certificats SSL, Apple et Google pour respectivement les applications iOS/MacOS et les applications Android, ou encore de nombreuses distributions Linux avec des signatures OpenPGP. C'est par exemple le cas de Debian : ce sont les deux fichiers que j'avais caché ci-dessus :

Elles sont également utilisées pour le traffic HTTPS avec là encore des certificats SLL, c'est ce qu'indique le cadenas dans la barre d'adresse de votre navigateur Internet. Enfin, si vous avez déjà signé des documents PDF "correctement" (càd pas en ajoutant seulement une image par-dessus), votre logiciel ajoute en fait au document PDF une signature numérique, qui permet de garantir deux choses : que quelqu'un avec votre clef a effectué la signature, et également quelle version du document a été signée, puisque toute modification rend alors la signature invalide.

Cette signature a d'ailleurs une valeur légale en France depuis 2000, avec une standardisation à l'échelle européenne en 2016. C'est ce qui permet la signature de contrats sur Internet en passant par des sites spécialisés, qui apposent alors leur propre signature numérique en votre nom.

En ce qui concerne la vérification de l'authenticité des signatures mêmes (et donc des clefs), on retrouve plusieurs modes de fonctionnement, dont pour les plus importants :

• La toile de confiance : ce sont les autres utilisateurs qui certifient l'authenticité des clefs, chaque utilisateur pouvant dire, en apposant sa signature, si une clef appartient bien à l'utilisateur qui dit la posséder. Il s'agit donc d'un système dit décentralisé, il n'y a pas une entité centrale qui contrôle tout.
• La blockchain. Je vous invite à vous réferrer aux MONs cités ci-dessus pour son fonctionnement. L'idée est là que la blockchain elle-même, par son fonctionnement, garantit l'authenticité des données qu'elle contient, et donc des associations utilisateurs-clefs. Là aussi, c'est un système décentralisé.
• Les autorités de certifications. Ici, il s'agit d'un système centralisé : la confiance est initialement placée dans une entité très puissante, qui se charge de distribuer et certifier l'authenticité des certificats. En pratique, les autorités de certifications vont désigner des autorités de certifications plus petites, puisqu'elles ne peuvent évidemment pas traiter toutes les demandes. C'est ce qui est utilisé pour les certificats SSL. Par exemple, le certificat du site centrale-mediterranee.fr provient de l'entreprise GÉANT, qui possède elle-même un certificat émanant de USERTrust RSA Certification Authority.

Références

• Wikipédia
• Le cours de sécurité de M. Brucker (https://francoisbrucker.github.io/cours_informatique/cours/sécurité/)
• La signature électronique : un outil devenu incontournable sur Francenum.gouv.fr
• RFC Editor, qui héberge les RFC, les documents décrivant notamment les standards en vigueur sur Internet
• Suivez les 10 principes ALCOA++, sur le site de Mettler-Toledo
• La chaîne Youtube Ben Eater, qui a quelques vidéos traitant de la détection d'erreurs et sur certains protocoles qui en font usage